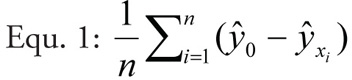
(C) 2011 Jan Thiele. This is an open access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
For reference, use of the paginated PDF or printed version of this article is recommended.
Prioritisation of high-impact species is becoming increasingly important for management of introduced species (‘neobiota’) because of their growing number of which, however, only a small fraction has substantial impacts. Impact scores for prioritising species may be affected by the type of effect model used. Recent studies have shown that environmental co-variation and non-linearity may be significant for effect models of biological invasions. Here, we test for differences in impact scores between simple and complex effect models of three invasive plant species (Heracleum mantegazzianum, Lupinus polyphyllus, Rosa rugosa).
We investigated the effects of cover percentages of the invasive plants on species richness of invaded communities using both simple linear effect models (‘basic models’) and more complex linear or non-linear models including environmental co-factors (‘full models’). Then, we calculated impact scores for each invasive species as the average reduction of species richness predicted by basic and full effect models.
All three non-native species had negative effects on species richness, but the full effect models also indicated significant influence of habitat types. Heracleum mantegazzianum had uniform linear effects in all habitats, while effects of Lupinus polyphyllus interacted strongly with habitat type, and Rosa rugosa showed a marked non-linear relationship. Impact scores were overestimated by basic effect models for Heracleum mantegazzianum and Rosa rugosa due to disregard of habitat effects and non-linearity, respectively. In contrast, impact of Lupinus polyphyllus was underestimated by the basic model that did not account for the strong interaction of invader cover and habitat type.
We conclude that simple linear models will often yield inaccurate impact scores of non-native species. Hence, effect models should consider environmental co-variation and, if necessary, non-linearity of the effects of biological invasions on native ecosystems.
effect model, Heracleum mantegazzianum, impact assessment, Lupinus polyphyllus, management, non-native, prioritisation, Rosa rugosa
Impacts differ in quality and quantity among introduced species (‘neobiota’). Many non-indigenous species can be considered neutral, but some have severe implications for native biodiversity, ecosystems, human health and economy (Gaertner et al. 2009, Hejda et al. 2009, Goodenough 2010). Globally, roughly 1% of the introduced species have become invasive with substantial impacts (i.e. invaders sensu Davis and Thompson 2000), but this proportion varies among regions and is likely to increase with longer residence times (Williamson 1996, Richardson and Pysek 2006). The human and financial resources available for management of biological invasions do not allow controlling all invasive species. Hence, it is increasingly necessary to prioritise management of neobiota according to rankings of their impacts (Parker et al. 1999, Byers et al. 2002, Thiele et al. 2010a).
Different approaches have been taken to study the impact of invasive species. Regarding species richness of invaded communities, for instance, removal or seed-addition experiments have been used (Meffin et al. 2010), as well as comparisons of invaded and uninvaded sites (Adams and Engelhardt 2009, Hejda et al. 2009, Flory and Clay 2010, Maurel et al. 2010), multi-year studies of expanding margins of invasive stands (Brewer 2008), comparisons of different stages of invasion (Prévosto et al. 2006), and correlational studies of gradients of invader abundance (Isermann et al. 2007, Gooden et al. 2009). All these approaches have their pros and cons concerning inference about invader impacts (cf. Adams and Engelhardt 2009, Meffin et al. 2010).
For impact assessment, according to the framework provided by Parker et al. (1999), and expanded by Thiele et al. (2010a), it is advantageous to relate invader effects to direct measures of invader abundance or equivalent measures, because the density of stands of a specific invasive species and the consequent impacts may vary among invaded sites, forming continuous gradients. Further, the relationship of effect and invader abundance may be non-linear which may affect impact estimates and also management decisions (Yokomizo et al. 2009).
Relationships of invader abundance and ecosystem traits may be modified by environmental factors (Houlahan and Findlay 2004, Surrette and Brewer 2008), so that one actually has to deal with a triangular relationship. A negative correlation may partly be the result of environmental conditions facilitating the invasion, while constraining the ecosystem trait. For instance, disturbance events that destroy most biomass of a given plant community may reduce species numbers, but could increase the abundance of invasive plant species. So, a negative relationship of invader abundance and species richness among sites with different disturbance regimes may be caused by environmental factors, instead of being a genuine effect of the invader. Moreover, effects of an invasive species on a particular ecosystem trait often vary among habitat types. For example, invasion of a tree species may decrease the cover of native herbaceous plants in a formerly treeless habitat, whereas it even could facilitate native species in forests, as has been shown for Cinchona spp. (Fischer et al. 2009, Jäger et al. 2009). Different or contrasting effects can be modelled as interactions of invader abundance and habitat type. Although it is important to include environmental variables into effect models of invasive species, the potential strength of the influence of environmental variation on impact scores has rarely been tested.
The aim of the present study was to assess to which extent impact scores of invasive species are affected by environmental variation, and by choice of a linear vs. non-linear effect model. We used empirical data of three invasive plant species for model building and calculation of impact scores. Richness of vascular plant species of invaded communities was chosen as response variable.
Methods Study species and field dataWe used three plant species, Heracleum mantegazzianum, Lupinus polyphyllus and Rosa rugosa, that are invasive and widespread in Europe; all three are able to form dominant stands with >90% cover (Thiele et al. 2010b).
Heracleum mantegazzianum (Apiaceae) is a monocarpic tall herb native to the Western Greater Caucasus. It invades mesic grasslands, waste ground, riverbanks, roadsides and forest edges where it forms tall-herb stands (Tiley et al. 1996, Pyšek et al. 2007).
Lupinus polyphyllus (Fabaceae) is a nitrogen-fixing perennial tall herb from Pacific North America that spreads by seeds and rhizomes. In Central Europe, it mainly invades unimproved and mesic grasslands in mountain areas and transforms them into tall-herb stands, especially when grassland management is abandoned (Otte et al. 2002, Otte and Maul 2005).
Rosa rugosa (Rosaceae) is a shrub originating from the Pacific coasts of East Asia. In Europe, it mainly invades coastal habitats, but it can also become invasive on inland habitats, such as Calluna heath (Bruun 2005, Kollmann et al. 2007, Isermann 2008, Thiele et al. 2009).
We estimated cover percentages of the invasive study species and recorded all vascular plant species on plots of 16, 25 or 100 m² (see Table 1) that were established in different communities invaded by the study species. In Heracleum mantegazzianum all plots were situated inside of invaded areas, while in Lupinus polyphyllus and Rosa rugosa, sampling also included areas adjacent to invaded stands, but still inside of the same plant community. Cover percentages of the invaders ranged between zero and (almost) 100% percent. Details on the datasets are given in Table 1.
Characteristics of the datasets used for effect modelling and for calculating impact scores.
| Heracleum mantegazzianum | Lupinus polyphyllus | Rosa rugosa | |
|---|---|---|---|
| Plot size (m²) | 25 | 25, 100 | 16 |
| No. of plots | 202 | 80 | 63 |
| Sampling years | 2002, 2003 | 1998, 2001 | 2001 |
| Invader cover (%) | |||
| Minimum | 1 | 0 | 0 |
| Mean | 37 | 22 | 44 |
| Maximum | 95 | 90 | 100 |
| Study regions | Western, central and southern Germany (22 areas) | Central Germany (Rhön mountains) | Northwestern Germany (Spiekeroog, Norderney, Juist) |
| Heracleum mantegazzianum | Lupinus polyphyllus | Rosa rugosa | |
|---|---|---|---|
| Plot size (m²) | 25 | 25, 100 | 16 |
| No. of plots | 202 | 80 | 63 |
| Sampling years | 2002, 2003 | 1998, 2001 | 2001 |
| Invader cover (%) | |||
| Minimum | 1 | 0 | 0 |
| Mean | 37 | 22 | 44 |
| Maximum | 95 | 90 | 100 |
| Study regions | Western, central and southern Germany (22 areas) | Central Germany (Rhön mountains) | Northwestern Germany (Spiekeroog, Norderney, Juist) |
The plots were assigned to habitat types based on plant communities of Central Europe (see Ellenberg 2009) or, in few cases, based on physiognomy, land use and disturbance regime where assignment to plant communities by floristic composition was not feasible. Definitions of habitat types are given in the Supplement (Table A1).
Effect modellingFirst, we calculated ‘basic’ effect models that only contained invader cover as predictor of species richness. For all three invaders, species counts within the plots clearly deviated from normal distributions. Thus, we used Generalized Linear Models (GLM) with (quasi-)Poisson distribution and log-link which fitted the data well.
Next, we looked for the best models of species richness considering invader cover, habitat type, squared invader cover and interactions of (squared) invader cover with habitat type, as potential predictor variables. We tested the significance of predictor variables with likelihood ratio tests, starting with the basic model (‘invader cover’) and adding one additional predictor variable at a time, in the aforementioned sequence. Only variables that significantly improved the model fit were included in the final effect model (‘full model’). All effect models were calculated with R 2.10.1 (R Development Core Team 2009).
The models of Lupinus polyphyllus included plot size as an additional predictor variable to account for the possibility that 100-m² plots contained more species than 25-m² plots because of species-area relationships. For Rosa rugosa, we calculated Generalized Linear Mixed Models (GLMM) that included a random site effect to account for nestedness of the plots. The GLMM were calculated with ‘lmer’ of the ‘lme4’ package in R.
Calculation of impact scoresWe calculated impact scores by averaging predicted species loss over all sample sites using the basic and full models, thus yielding two impact scores per invasive species. Impact scores were calculated as the difference between predicted species richness at zero invader cover and predicted richness given the actual cover of the invader, averaged over all plots for each invasive species (see Equ. 1).
where ŷ = predicted species richness, xi = invader cover of site i, and n = number of sample plots per invasive species.
For calculation of the predicted species richness, we used estimates of all predictor variables in the model. If habitat type was a significant predictor, we used estimates of all habitat categories in the calculations, even if the estimates of some categories did not differ significantly from zero according to the GLM t test or z test.
We calculated percentile (2.5–97.5%) confidence intervals for impact scores with bootstrapping using 10, 000 resamples with replacement of same size as the original sample.
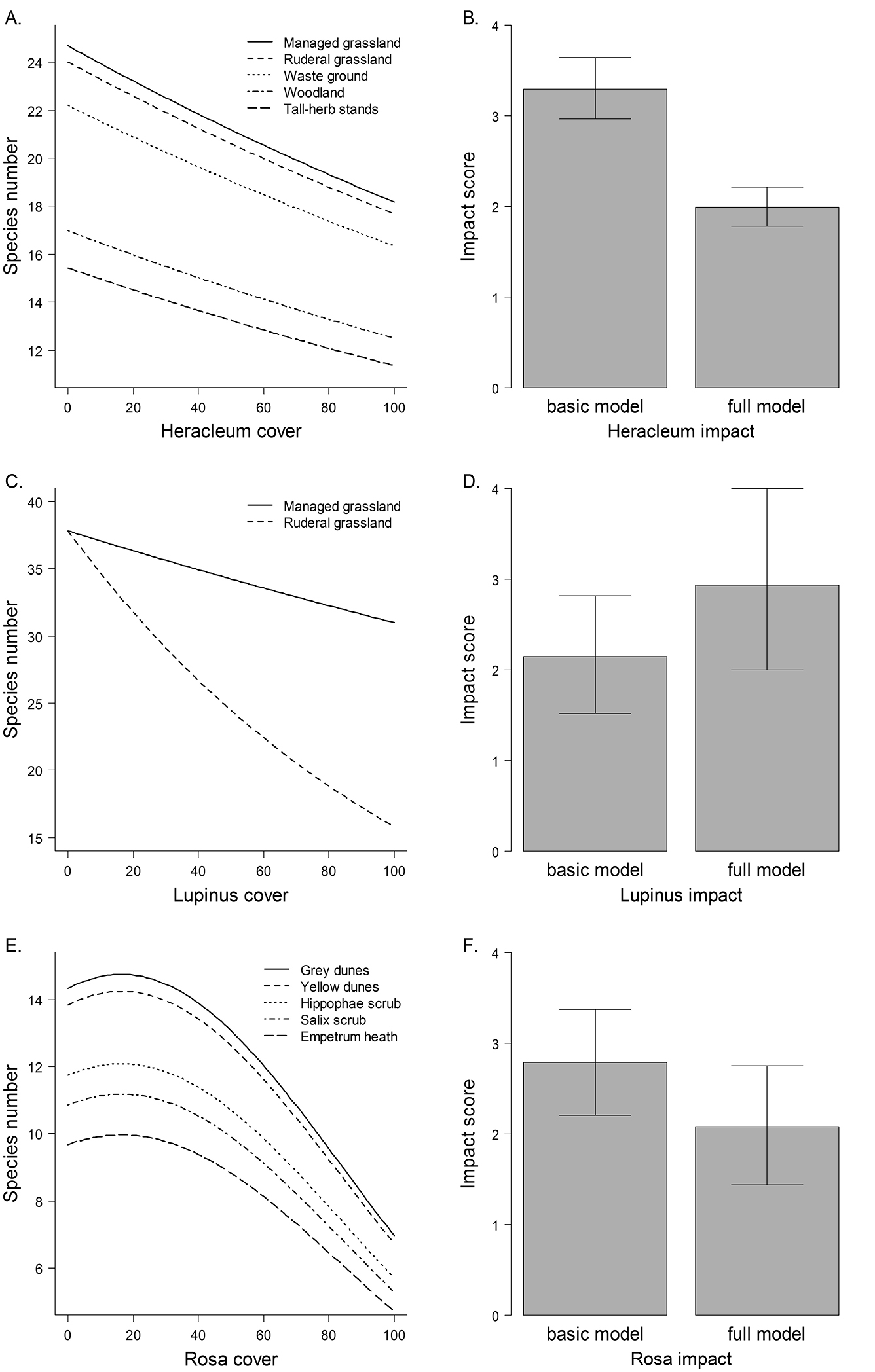
ResultsWe found different effect models for the three invasive species (Table 2, Figure 1). Models of Heracleum mantegazzianum and Rosa rugosa contained main effects of habitat types, indicating that habitat types differed in species richness. Among habitat types invaded by Lupinus polyphyllus, i.e. ruderal and managed grasslands, species richness differed not per se, but the relationship of invader cover and species richness interacted with habitat type (Figure 1c).
Components of ‘full’ effect models. P-values are taken from sequential Likelihood Ratio tests. Signs (–, +) indicate the relationship of (squared) invader cover with species richness; NS, not significant.
| Variable | Heracleum mantegazzianum | Lupinus polyphyllus | Rosa rugosa |
|---|---|---|---|
| Invader cover | (–) < 0.001 | (–) 0.018 | (+) < 0.001 |
| Habitat type | < 0.001 | †NS | 0.021 |
| Squared invader cover | NS | NS | (–) 0.015 |
| Habitat type x invader cover | NS | 0.004 | NS |
| Hab. type x squared inv. cover | NS | NS | NS |
| Variable | Heracleum mantegazzianum | Lupinus polyphyllus | Rosa rugosa |
|---|---|---|---|
| Invader cover | (–) < 0.001 | (–) 0.018 | (+) < 0.001 |
| Habitat type | < 0.001 | †NS | 0.021 |
| Squared invader cover | NS | NS | (–) 0.015 |
| Habitat type x invader cover | NS | 0.004 | NS |
| Hab. type x squared inv. cover | NS | NS | NS |
† Habitat type was marginally significant in sequential likelihood ratio tests when added after Lupinus polyphyllus cover and before squared Lupinus polyphyllus cover and the interaction terms (p = 0.033), but the main effect of habitat type did not improve the ‘full’ model that contained Lupinus cover and the interaction of cover and habitat type (p = 0.833).
The three invaders had negative effects on vascular plant species richness of invaded communities, but the shapes of the relationships differed. Heracleum mantegazzianum had uniform linear effects in all habitat types, while the effects of Lupinus polyphyllus were much stronger in ruderal than in managed grasslands. Rosa rugosa showed a non-linear relationship, so that species richness only was reduced at high cover percentages (Figure 1e). The details of the basic and full models (estimates etc.) are given in the Supplement (Tables A2–4).
Effect models and impact scores. Left panels show the ‘full’ effect models of Heracleum mantegazzianum (A), Lupinus polyphyllus (C) and Rosa rugosa (E) that included habitat type as a co-factor and, if significant, non-linear terms of cover percentages of the invasive species. Right panels (B, D, F) show the corresponding impact scores calculated with ‘full’ models and with ‘basic’ models that only included a linear term of invader cover.
Effect models and impact scores. Left panels show the ‘full’ effect models of Heracleum mantegazzianum (A), Lupinus polyphyllus (C) and Rosa rugosa (E) that included habitat type as a co-factor and, if significant, non-linear terms of cover percentages of the invasive species. Right panels (B, D, F) show the corresponding impact scores calculated with ‘full’ models and with ‘basic’ models that only included a linear term of invader cover.
Impact scores differed markedly between basic and full models (Figure 1). For the basic and full model of Heracleum mantegazzianum, confidence intervals of impacts scores did not overlap, indicating that part of the apparent effect on species richness predicted by the basic model was, indeed, due to general differences in species richness between invaded habitat types. For Lupinus polyphyllus and Rosa rugosa, impact scores calculated with full models were just outside the confidence intervals of the basic models, suggesting significant differences between model variants, but the confidence intervals overlapped by roughly 50%. Impact scores of Lupinus polyphyllus tended to be higher when taking the stronger effect in ruderal grasslands into account, whereas impact scores of Rosa rugosa tended to be lower when considering non-linear effects and general differences in species richness between invaded habitat types.
DiscussionThe case studies presented here show that effect models of invasive species may take various forms. Concerning impacts on biodiversity, models should consider environmental variation, because general biodiversity trends along ecological gradients may lead us to believe that impacts are higher than they actually are. However, underestimation of impacts may happen as well.
For instance, Heracleum mantegazzianum invades managed grasslands, ruderal (abandoned) grasslands and tall-herb stands – these habitat types resemble, and quite often are, a successional sere (Thiele and Otte 2006). Along this sere, species richness generally decreases, while average cover of Heracleum mantegazzianum increases. Only part of the decline in species richness is attributable to Heracleum mantegazzianum that shades out lower growing grassland plants (Thiele et al. 2010b), while another part is due to generally lower species numbers in tall-herb stands compared to the grasslands that they replace during succession (Neuhäusl and Neuhäuslova-Novotna 1985). In other words, species numbers of tall-herb stands are low even if Heracleum mantegazzianum covers only a minor proportion of the area. In contrast, impact of Lupinus polyphyllus was underestimated using a simple model that included no potential interactions of invader cover and habitat type. In fact, reduction of species richness was much stronger in ruderal than managed grasslands. Hence, inclusion of the interaction term increased the impact score, although ruderal grasslands represented only 25% of the plots sampled.
Several recent studies have found that inclusion of environmental variables into effect models changed predictions of invader effects on biodiversity: apparent negative effects of Lythrum salicaria L. and Rhamnus frangula L. on richness of rare native species disappeared (Houlahan and Findlay 2004), negative correlation of Lonicera japonica Thunb. with species richness became less strong (Surrette and Brewer 2008), but on the other side, effect estimates of (native) Hippophaë rhamnoides increased, i.e. became more negative, by up to 50% when including environmental co-variables (Isermann et al. 2007). Further, Spartina anglica C.E. Hubb. reduces native species richness in low-salinity marshes, while facilitating richness in mudflats (Hacker and Dethier 2006), and differences in impact on species richness among sites (Mediterranean islands) have been found for Ailanthus altissima (Mill.) Swingle and Oxalis pes-caprae L. (Vilá et al. 2006). Hence, it is the rule rather than an exception that disregarding environmental co-variation leads to biased estimates of invader effects on species richness.
Also non-linear relationships between invader abundance and biodiversity can substantially influence impact assessments. In the case of Rosa rugosa, the impact score was lower when introducing a quadratic term into the effect model, while inclusion of habitat type did not change the score much (basic model, 2.8; habitat model, 2.9; quadratic model, 2.1). A non-linear increase of effect with invader abundance will commonly lead to higher impact scores compared to a linear model (Thiele et al. 2010a), but the model of Rosa rugosa included both a negative quadratic and a positive linear term, so that in fact the non-linear model predicted a lesser effect. Non-linear effects on species richness were also found for the shrubs Lantana camara L. (Gooden et al. 2009) and Hippophaë rhamnoides (Isermann et al. 2007). These results suggest that non-linearity of abundance-effect relationships of invasive species should be considered in future impact studies.
Further advances of impact assessment and a deeper understanding of invader-diversity relationships could be expected from studies that take traits of the resident species into account, e.g. by modelling richness of functional plant groups or of species of high-conservation value. For the invaders studied here, it has been shown that different plant types – size classes, life forms, sociological groups – are affected differently (Thiele et al. 2010b). Regarding theory of biological invasions it would be interesting to investigate whether or not impact models could be generalised within groups of invasive species (e.g. life forms or strategy types). Another question is how to represent environmental variation in effect models. Here, we used habitat type as a co-factor which appears practical and useful, but might not be the optimal solution. The suitability of environmental properties and scaling of the variables (metric, categorical) will depend on both the invasive species and the ecosystem trait under study. Finally, multiple regression models, as applied here, account for main effects and interactions of invader and environment, but do not consider possible correlations among them. Thus, effect estimates may still be affected by spurious correlations. Further improvements could be achieved by more advanced models using, e.g., corrected path coefficients instead of regression coefficients.
Besides scientific approaches, impact assessment is grounded in normative definitions of impact or ecological damage. Not all negative relationships of invasive species with ecosystem traits necessarily have to be considered as damage, but definitions might focus on legal conservation resources or set thresholds discerning minor adverse effects from ‘significant’ damage (Bartz et al. 2010). In a normative sense, changes in species numbers may not directly quantify the ensuing damage (Ingo Kowarik, pers. comm.). Merging scientific and normative approaches into practical implementations of impact assessment of invasive species remains a challenge for applied invasion biology and environmental planning.
ConclusionsSimple linear effect models may often yield inaccurate impact scores of invasive species. Hence, it appears to be advisable to consider somewhat more complex models that include environmental co-variables and, if applicable, non-linear effect terms. Models should preferentially be based on samples representing the full environmental gradient of invaded habitats and the full range of equilibrium abundances or cover percentages of the invasive species.
The study on Heracleum mantegazzianum by JT and AO was funded by the European Union within the project ‘Giant Alien’ (EVK2-CT-2001-00128). Research by JK benefited from a grant by the University of Copenhagen (‘Centre for Invasive Species’). We thank Franz Essl and Ingo Kowarik for helpful comments on an earlier version of the manuscript.
Definitions of habitat types. For descriptions of plant communities (syntaxa) see Ellenberg (2009).
| Species | Habitat type | Definition |
|---|---|---|
| Heracleum mantegazzianum | Managed grassland | Pastures and meadows of well drained, fertile soils (typical Arrhenatheretalia communities) |
| Ruderal grassland | Abandoned grassland, field margins, road verges and embankments (Arrhenatheretalia communities containing characteristic species of Galio-Urticetea and Artemisietea) | |
| Tall-herb communities | Tall-herb communities of fertile soils (Galio-Urticetea) | |
| Waste ground | Open communities of disturbed, non-agricultural sites (e.g. abandoned sand pits); floristic composition not matching any particular syntaxon | |
| Woodland | Communities dominated by trees; alluvial woodland (Alnenion-glutinoso incanae, Salicion eleagni), copses and anthropogenic (semi-open) forests | |
| Lupinus polyphyllus | Managed grassland | Unimproved Nardus grassland (Violion caninae) and montane grassland of more fertile soils (Polygono-Trisetion) with current or recent grassland management (mowing, grazing) |
| Ruderal grassland | Unimproved Nardus grassland (Violion caninae) and montane grassland of more fertile soils (Polygono-Trisetion) without current land use containing characteristic species of tall-herb communities (Galio-Urticetea); subordinately sedge fens (Caricetum nigrae) | |
| Rosa rugosa | Yellow dune | Mobile yellow dunes dominated by Ammophila arenaria (Ammophiletea: Elymo-Ammophiletum) |
| Grey dune | Semi-fixed and fixed grey dunes with short, open grasslands (Koelerio-Corynephoretea), especially Corynephorion canescentis, Violo-Corynephoretum as well as herb-rich communities of the Tortulo-Koelerion | |
| Hippophaë scrub | Hippophaë rhamnoides scrub on semi-fixed grey dunes (Rhamno-Prunetea: Hippophao–Sambucetum) | |
| Salix scrub | Salix repens dominated scrub on dry fixed dunes (mainly brown dunes) mostly belonging to the Salici repentis-Empetretum (Empetrion nigri) | |
| Empetrum heath | Empetrum nigrum dominated heathlands on brown dunes (Empetrion nigri: Carici arenariae-Empetretum and Polypodio-Empetretum) |
| Species | Habitat type | Definition |
|---|---|---|
| Heracleum mantegazzianum | Managed grassland | Pastures and meadows of well drained, fertile soils (typical Arrhenatheretalia communities) |
| Ruderal grassland | Abandoned grassland, field margins, road verges and embankments (Arrhenatheretalia communities containing characteristic species of Galio-Urticetea and Artemisietea) | |
| Tall-herb communities | Tall-herb communities of fertile soils (Galio-Urticetea) | |
| Waste ground | Open communities of disturbed, non-agricultural sites (e.g. abandoned sand pits); floristic composition not matching any particular syntaxon | |
| Woodland | Communities dominated by trees; alluvial woodland (Alnenion-glutinoso incanae, Salicion eleagni), copses and anthropogenic (semi-open) forests | |
| Lupinus polyphyllus | Managed grassland | Unimproved Nardus grassland (Violion caninae) and montane grassland of more fertile soils (Polygono-Trisetion) with current or recent grassland management (mowing, grazing) |
| Ruderal grassland | Unimproved Nardus grassland (Violion caninae) and montane grassland of more fertile soils (Polygono-Trisetion) without current land use containing characteristic species of tall-herb communities (Galio-Urticetea); subordinately sedge fens (Caricetum nigrae) | |
| Rosa rugosa | Yellow dune | Mobile yellow dunes dominated by Ammophila arenaria (Ammophiletea: Elymo-Ammophiletum) |
| Grey dune | Semi-fixed and fixed grey dunes with short, open grasslands (Koelerio-Corynephoretea), especially Corynephorion canescentis, Violo-Corynephoretum as well as herb-rich communities of the Tortulo-Koelerion | |
| Hippophaë scrub | Hippophaë rhamnoides scrub on semi-fixed grey dunes (Rhamno-Prunetea: Hippophao–Sambucetum) | |
| Salix scrub | Salix repens dominated scrub on dry fixed dunes (mainly brown dunes) mostly belonging to the Salici repentis-Empetretum (Empetrion nigri) | |
| Empetrum heath | Empetrum nigrum dominated heathlands on brown dunes (Empetrion nigri: Carici arenariae-Empetretum and Polypodio-Empetretum) |
Table A2. Effect models of Heracleum mantegazzianum (Generalized Linear Models with quasi-Poisson distribution and log-link).
| A. Basic model | ||||
|---|---|---|---|---|
| Model component | Estimate | Std. Error | t value | Pr(>|t|) |
| Intercept | 3.0596 | 0.0496 | 61.7 | < 0.001 |
| Heracleum mantegazzianum cover | -0.0048 | 0.0011 | -4.2 | < 0.001 |
| Null deviance: 842.0 on 201 degrees of freedomResidual deviance: 771.7 on 200 degrees of freedom | ||||
| B. Full model | ||||
| Model component | Estimate | Std. Error | t value | Pr(>|t|) |
| Intercept | 3.2064 | 0.0632 | 50.7 | < 0.001 |
| Heracleum mantegazzianum cover | -0.0031 | 0.0012 | -2.6 | 0.009 |
| Habitat: ruderal grassland | -0.0276 | 0.0857 | -0.3 | 0.748 |
| Habitat: tall-herb stands | -0.4701 | 0.0888 | -5.3 | < 0.001 |
| Habitat: waste ground | -0.1062 | 0.1132 | -0.9 | 0.349 |
| Habitat: woodland | -0.3745 | 0.1183 | -3.2 | 0.002 |
| Null deviance: 842.0 on 201 degrees of freedomResidual deviance: 622.0 on 196 degrees of freedom | ||||
| A. Basic model | ||||
|---|---|---|---|---|
| Model component | Estimate | Std. Error | t value | Pr(>|t|) |
| Intercept | 3.0596 | 0.0496 | 61.7 | < 0.001 |
| Heracleum mantegazzianum cover | -0.0048 | 0.0011 | -4.2 | < 0.001 |
| Null deviance: 842.0 on 201 degrees of freedomResidual deviance: 771.7 on 200 degrees of freedom | ||||
| B. Full model | ||||
| Model component | Estimate | Std. Error | t value | Pr(>|t|) |
| Intercept | 3.2064 | 0.0632 | 50.7 | < 0.001 |
| Heracleum mantegazzianum cover | -0.0031 | 0.0012 | -2.6 | 0.009 |
| Habitat: ruderal grassland | -0.0276 | 0.0857 | -0.3 | 0.748 |
| Habitat: tall-herb stands | -0.4701 | 0.0888 | -5.3 | < 0.001 |
| Habitat: waste ground | -0.1062 | 0.1132 | -0.9 | 0.349 |
| Habitat: woodland | -0.3745 | 0.1183 | -3.2 | 0.002 |
| Null deviance: 842.0 on 201 degrees of freedomResidual deviance: 622.0 on 196 degrees of freedom | ||||
Table A3. Effect models of Lupinus polyphyllus (Generalized Linear Models with quasi-Poisson distribution and log-link).
| A. Basic model | ||||
|---|---|---|---|---|
| Model component | Estimate | Std. Error | t value | Pr(>|t|) |
| Intercept | 3.5844 | 0.0765 | 46.9 | < 0.001 |
| Lupinus polyphyllus cover | -0.0028 | 0.0012 | -2.3 | 0.024 |
| Plot size (25/ 100 m²) | 0.0017 | 0.0009 | 1.8 | 0.077 |
| Null deviance: 282.8 on 79 degrees of freedomResidual deviance: 234.3 on 77 degrees of freedom | ||||
| B. Full model | ||||
| Model component | Estimate | Std. Error | t value | Pr(>|t|) |
| Intercept | 3.6334 | 0.0744 | 48.9 | < 0.001 |
| Plot size (25/ 100 m²) | 0.0012 | 0.0009 | 1.3 | 0.201 |
| Lupinus polyphyllus cover | -0.0020 | 0.0012 | -1.7 | 0.089 |
| Habitat: ruderal grassland | -0.0067 | 0.0023 | -2.9 | 0.005 |
| Null deviance: 282.8 on 79 degrees of freedomResidual deviance: 210.6 on 76 degrees of freedom | ||||
| A. Basic model | ||||
|---|---|---|---|---|
| Model component | Estimate | Std. Error | t value | Pr(>|t|) |
| Intercept | 3.5844 | 0.0765 | 46.9 | < 0.001 |
| Lupinus polyphyllus cover | -0.0028 | 0.0012 | -2.3 | 0.024 |
| Plot size (25/ 100 m²) | 0.0017 | 0.0009 | 1.8 | 0.077 |
| Null deviance: 282.8 on 79 degrees of freedomResidual deviance: 234.3 on 77 degrees of freedom | ||||
| B. Full model | ||||
| Model component | Estimate | Std. Error | t value | Pr(>|t|) |
| Intercept | 3.6334 | 0.0744 | 48.9 | < 0.001 |
| Plot size (25/ 100 m²) | 0.0012 | 0.0009 | 1.3 | 0.201 |
| Lupinus polyphyllus cover | -0.0020 | 0.0012 | -1.7 | 0.089 |
| Habitat: ruderal grassland | -0.0067 | 0.0023 | -2.9 | 0.005 |
| Null deviance: 282.8 on 79 degrees of freedomResidual deviance: 210.6 on 76 degrees of freedom | ||||
Table A4. Effect models of Rosa rugosa (Generalized Linear Mixed Models with Poisson distribution and log-link, calculated with “lmer” of the “lme4” package in R).
| A. Basic model | ||||
|---|---|---|---|---|
| Model component | Estimate | Std. Error | z value | Pr(>|z|) |
| Intercept | 2.5547 | 0.0659 | 38.8 | < 0.001 |
| Rosa rugosa cover | -0.0061 | 0.0011 | -5.8 | < 0.001 |
| Null deviance: 113.6Residual deviance: 79.3 | ||||
| B. Full model | ||||
| Model component | Estimate | Std. Error | z value | Pr(>|z|) |
| Intercept | 2.2515 | 0.2209 | 10.2 | < 0.001 |
| Rosa rugosa cover | 0.0035 | 0.0041 | 0.9 | 0.391 |
| Habitat: grey dunes | 0.0348 | 0.1316 | 0.3 | 0.791 |
| Habitat: Empetrum heath | -0.3572 | 0.1463 | -2.4 | 0.015 |
| Habitat: Hippophaë scrub | -0.1643 | 0.1486 | -1.1 | 0.269 |
| Habitat: Salix scrub | -0.2423 | 0.1907 | -1.3 | 0.204 |
| Squared Rosa rugosa cover | -0.4155 | 0.1684 | -2.5 | 0.014 |
| Null deviance: 113.6Residual deviance: 61.8 | ||||
| A. Basic model | ||||
|---|---|---|---|---|
| Model component | Estimate | Std. Error | z value | Pr(>|z|) |
| Intercept | 2.5547 | 0.0659 | 38.8 | < 0.001 |
| Rosa rugosa cover | -0.0061 | 0.0011 | -5.8 | < 0.001 |
| Null deviance: 113.6Residual deviance: 79.3 | ||||
| B. Full model | ||||
| Model component | Estimate | Std. Error | z value | Pr(>|z|) |
| Intercept | 2.2515 | 0.2209 | 10.2 | < 0.001 |
| Rosa rugosa cover | 0.0035 | 0.0041 | 0.9 | 0.391 |
| Habitat: grey dunes | 0.0348 | 0.1316 | 0.3 | 0.791 |
| Habitat: Empetrum heath | -0.3572 | 0.1463 | -2.4 | 0.015 |
| Habitat: Hippophaë scrub | -0.1643 | 0.1486 | -1.1 | 0.269 |
| Habitat: Salix scrub | -0.2423 | 0.1907 | -1.3 | 0.204 |
| Squared Rosa rugosa cover | -0.4155 | 0.1684 | -2.5 | 0.014 |
| Null deviance: 113.6Residual deviance: 61.8 | ||||